Have you ever stopped to think about the edges of things around you? Like, what if you needed to put a fence around your backyard, or maybe you wanted to walk the exact distance around a big, open field? That idea of measuring the outside edge of something is actually a pretty important concept, and it's called "perimeter." It's a way to figure out just how much "around" there is, so you know, for instance, how much material you might need for that fence, or how far your stroll will be.
Figuring out this distance, this "perimeter," is a pretty basic but powerful skill, too. It helps us make sense of the size of things, not in terms of how much space they take up inside, but how long their outer shell is. Whether you are working with a simple square, a long rectangle, or even a perfectly round circle, there is a way to calculate that outside measurement. It’s a fundamental idea that shows up in all sorts of places, from school assignments to building projects, so it's almost always good to have a grasp of it.
This idea of the "perimeter formula" is really about understanding the different ways we can count up those outer lengths. We'll explore what perimeter means, how it's different from other measurements, and, you know, how we apply it to all sorts of shapes you might come across. We'll even look at some interesting real-world situations where knowing how to find the perimeter comes in handy, like when you're thinking about a package you need to send, or even the shape of a window in your home. It’s pretty straightforward once you get the hang of it, actually.
What is the Perimeter Formula, Really?
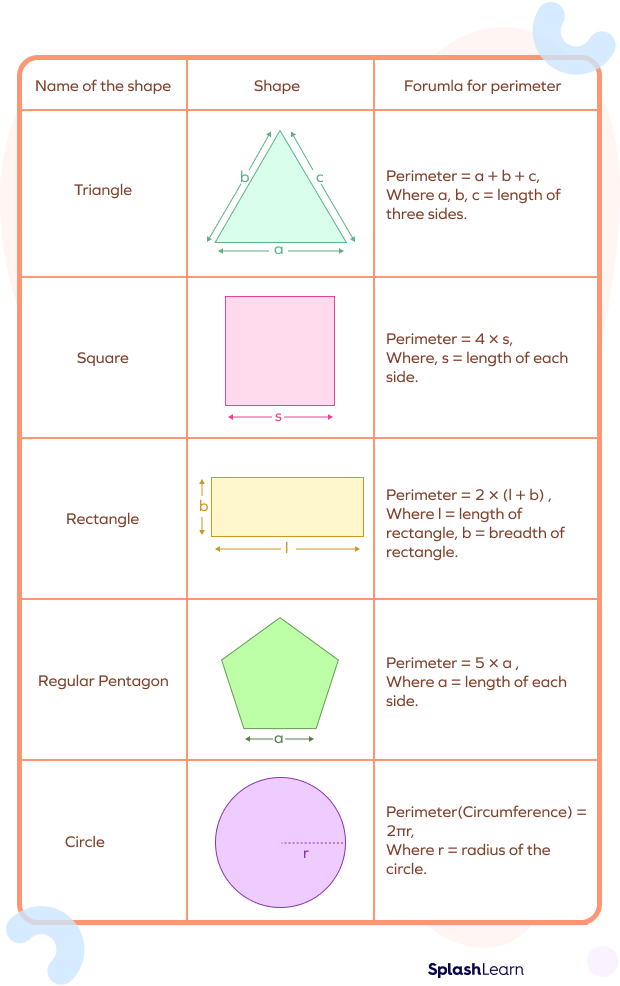
So, what exactly are we talking about when we say "perimeter formula"? At its heart, perimeter is simply the entire distance around the outside edge of any given shape. Imagine you are drawing a line along the border of something; the length of that line, when you get back to where you started, is its perimeter. We usually represent this measurement with the letter 'p', which is pretty convenient, really. It’s a way of defining the size of a shape by its boundary, which is a bit different from thinking about the space it covers.
It's important to remember that perimeter is distinct from something like "area." Area tells you how much flat space a shape takes up inside its boundaries, sort of like how much carpet you would need to cover a room. Area is measured in square units, like square meters or square inches. Perimeter, however, is a linear measurement. It’s like measuring a length of string, so its units are simple lengths, such as meters, centimeters, inches, or feet. Knowing this difference is pretty key, because, you know, they tell us very different things about a shape.
How Do We Find the Distance Around a Shape?
For shapes with straight sides, like a triangle, a square, or a rectangle, figuring out the perimeter formula is pretty much just a matter of adding up the lengths of all those sides. For example, if you have a square plot of land where each side measures ten inches, then its total distance around would be ten plus ten plus ten plus ten, which gives you forty inches. That's a square with a perimeter of forty inches, just like the one mentioned in "My text." It’s really that simple for many common figures, actually.
When you are looking at shapes that are drawn on a coordinate plane, where points are given by numbers, you might need a little extra step. To determine the lengths of those sides, you'll use what's called the distance formula. Once you have the length of each side, you just add them all together. This approach works for any polygon, whether it's a triangle, a pentagon, or something with even more sides. It’s just like walking around the edge and measuring each step, more or less.
Perimeter Formulas for Common Shapes
Different shapes, naturally, have their own ways of calculating this outer measurement, but they all stick to the basic idea of measuring the boundary. For a square, since all four sides are the same length, you just take the length of one side and multiply it by four. So, if a side is 's', the perimeter is '4s'. This is a very quick way to get the perimeter formula for a square. For a rectangle, which has two pairs of equal sides, you would add the length and the width together, and then multiply that sum by two. So, for a rectangle with length 'l' and width 'w', the perimeter is '2 times (l + w)', or '2l + 2w', as noted in "My text."
When it comes to a triangle, you simply add the lengths of its three sides. If it's a right triangle, where one angle is a perfect corner, you might use the Pythagorean theorem (a squared plus b squared equals c squared) to figure out a missing side length before adding them all up. For a circle, the distance around its edge has a special name: "circumference." The circumference is found using a specific perimeter formula involving its radius (the distance from the center to the edge) or its diameter (the distance straight across through the center). You multiply pi (a special number, roughly 3.14) by the diameter, or by two times the radius. So, it's either 'pi times d' or '2 times pi times r', which is pretty neat.
Other shapes, like parallelograms, trapezoids, or even octagons, follow the same general rule: you sum up the lengths of all their sides to get the perimeter. There are even calculators available that can help you with this, which, you know, makes things a bit easier sometimes. They are really just applying these same basic perimeter formulas for you. The key is always to identify the individual lengths that make up the outer edge and then combine them.
What About Those Tricky Shapes, Like a Norman Window?
Sometimes, shapes are a bit more complicated than just a simple square or circle. Think about a "Norman window," for instance, which is basically a rectangle with a semicircle sitting right on top of it. To find the perimeter of something like that, you need to break it down. You'd add up the three straight sides of the rectangular part that are exposed, plus the curved length of the semicircle. You wouldn't count the top side of the rectangle, because that's where the semicircle is attached, you see. For a Norman window with a perimeter of 38 feet, as described in "My text," or even one with a perimeter of 288 inches, figuring out its area or dimensions involves carefully applying the perimeter formula to each part.
Another interesting problem from "My text" talks about a rectangular piece of sheet metal with a perimeter of 50 centimeters that gets rolled into a cylinder with open ends. In this situation, the perimeter of the flat sheet becomes something else when it's transformed. The width of the sheet, for instance, might become the height of the cylinder, and the length of the sheet would become the circumference of the cylinder's base. So, the perimeter formula of the original shape helps you understand the dimensions of the new, rolled shape. It's a rather clever application of the idea, actually, showing how perimeter can be a starting point for figuring out other properties like volume.
Why Does Knowing the Perimeter Formula Matter in Real Life?
You might be wondering why all this talk about the perimeter formula is important outside of a math class. Well, it turns out that knowing how to figure out the distance around something is incredibly useful in a lot of everyday situations. It helps us plan, build, and even just understand the spaces we live in. It’s not just about abstract numbers; it’s about practical applications that make things work. It's pretty cool, actually, how often this simple concept comes up.
For example, if you're trying to figure out how much trim you need to go around a room, or how much ribbon to wrap around a gift, you're essentially calculating a perimeter. If you are a gardener, you might need to know the perimeter of your flower garden to figure out how much fencing material to buy. These are all real-world uses for the perimeter formula, helping us make good decisions about materials and space, so it's quite a handy skill to have.
Fencing a Garden or Walking a Park – Real-World Perimeter Formula
Let's say you have a lovely rectangular flower garden, and you want to put a fence around it to keep out curious critters. The length of the fence you would need is exactly the perimeter of that garden. You would measure the length of each side and then add them all up. Or, if it's a rectangle, you would use that '2 times (length plus width)' perimeter formula. This is a very common and practical use of the idea, really, showing how a math concept directly translates into a real-world task.
Similarly, imagine a rectangular shaped park with a paved sidewalk surrounding it. If you wanted to know the total distance you would have to walk if you went all the way around the park on that sidewalk, you would be figuring out the park's perimeter. It helps you understand the scale of things, and, you know, how much exercise you might get. This kind of calculation is, in some respects, very straightforward, but it's also incredibly useful for planning and understanding physical spaces.
Calculating for Packages and Other Everyday Objects
Another interesting application of the perimeter formula comes up when you're sending packages. Some delivery services have rules about the maximum combined length and "girth" of a package. Girth is actually the perimeter of a cross-section of the package. So, if you have a rectangular box, the girth would be the perimeter of one of its ends. If a package can have a maximum combined length and girth of 120 inches, as mentioned in "My text," you need to use the perimeter formula for that cross-section to make sure your package meets the requirements. It’s a bit like measuring a belt around the middle of a box, you see.
Even in more abstract problems, the perimeter formula comes into play. For instance, there's a problem in "My text" about determining the minimum perimeter of a triangle given a specific point. While that sounds a bit complex, it still relies on the fundamental idea of adding up side lengths. Or consider the problem of a right triangle where the radius of an inscribed circle is 5 and the hypotenuse is 19. To find the perimeter of that triangle, you'd still need to know all three side lengths, possibly using other geometric relationships alongside the basic perimeter concept. It shows how the core idea is pretty versatile, actually.
Getting a Handle on Perimeter Formulas – A Quick Review
So, to bring it all back together, the perimeter formula is really about finding the total distance that covers the boundary of a shape. It's the length of the outline, whether that shape is a simple square, a long rectangle, or even something with a curve like a circle. We use specific ways to calculate it for different figures, like multiplying a side by four for a square, or adding up all the individual side lengths for a polygon. For a circle, we call it circumference, and it involves pi and the radius or diameter. It's all about that outer measurement, which is, you know, quite different from the space inside.
The units for perimeter are always simple linear units, like centimeters, meters, or feet, because you're measuring a length, not an area. This is a very important distinction to remember. Whether you're trying to figure out how much longer the perimeter of one rectangle is compared to a square, or trying to find the dimensions that maximize the area of a window with a set perimeter, the core idea remains the same: you're working with the distance around the outside. It's a foundational concept in mathematics that has, in some respects, countless practical applications in our daily surroundings, which is pretty neat.